Kỹ thuật phân nhóm theo thứ bậc (Hierarchical Clustering Techniques)

Nguyễn Văn Chức – chucnv@ud.edu.vn

Trong kỹ thuật phân nhóm theo thứ bậc (Hierarchical Clustering Techniques), có 2 phương pháp chính đó là:

Agglomerative Aapproach (bottom up approach):  Ban đầu, chúng ta xem mỗi đối tượng là 1 nhóm (cluster) và nhóm 2 đối tượng gần nhất thành 1 cluster. Quá trình này lặp lại cho đến khi tất cả các đối tượng được nhóm vào 1 cluster cuối cùng.

Divisive Approach (top down approach): Quá trình ngược lại với Agglomerative Approach, ban đầu chúng ta xem tất cả các đối tượng thuộc cùng 1 cluster, sau đó tiến hành phân thành 2 nhóm con (thường dựa vào khoảng cách lớn nhất). Quá trình này được thực hiện cho đến khi mỗi nhóm chỉ còn 1 đối tượng.

Trong phần này sẽ giới thiệu kỹ thuật phân nhóm Agglomerative Approach

Các bước trong kỹ thuật phân cụm Agglomerative Approach như sau:

1.      Chuyển đổi các đặc trưng (thuộc tính - Features) của đối tượng (objects) vào ma trận khoảng cách

2.      Xem mỗi đối tượng là một cluster (chẳn hạn, nếu ta có 4 đối tượng, ban đầu chúng ta sẽ có 4 clusters)

3.      Lặp lại 2 bước sau cho đến khi số cluster bằng 1

a.       Gộp 2 cluster gần nhất

b.      Cập nhật ma trận khoảng cách

Thuật toán Agglomerative Hierarchical Clustering (gọi tắt là AHC) được mô tả như sau:

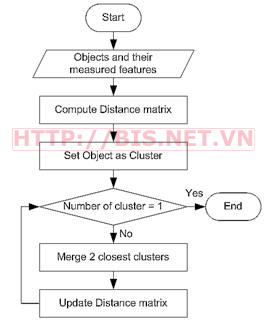
 Để hiểu hơn về thuật toán AHC, các bước của thuật toán AHC sẽ được minh họa thông qua ví dụ đơn giản sau.

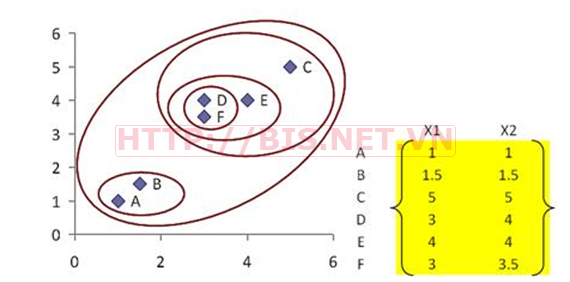
Giả sử ta có 6 đối tượng (objects) cần phân nhóm (tên của các đối tượng là A,B,C,D,E,F), mỗi đối tượng có 2 thuộc tính X1 và X2 như sau:

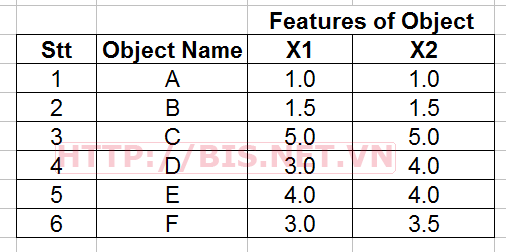
Chúng ta sẽ dùng thuật toán AHC để phân nhóm các đối tượng này

Chuyển sang ma trận khoảng cách (From Object Features to Distance Matrix)

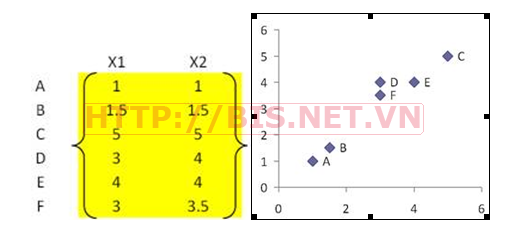
Khoảng cách giữa các đối tượng được biểu diễn bởi ma trận khoảng cách Dist. Khoảng cách Euclidean thường được dung để tính khoảng cách giữ 2 đối tượng như sau:

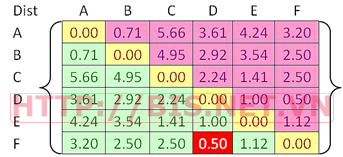
Chú ý: Dist là ma trận đối xứng qua đường chéo chính (vì khoảng cách từ A đến B bằng khoảng cách từ B đến A) nên chúng ta chỉ quan tâm đến phần bên trên hoặc bên dưới đường chéo chính. Trong ma trận khoảng cách, các phần tử trên đường chéo chính bằng 0 (khoảng cách đến chính nó).

Một cách tổng quát, nếu ta có m đối tượng, số khoảng cách giữa các đối tượng (bên trên hoặc bên dưới đường

 Bây giờ chúng ta đã có ma trận khoảng cách, công việc tiếp theo là tính liên kết giữa các đối tượng như sau:

Tính liên kết giữa các đối tượng (compute linkages between objects )

Có rất nhiều cách tính linkage, trong đó các cách sau đây thường được sử dụng

• Single Linkage: Khoảng cách giữa 2 clusters được tính là khoảng cách giữa 2 đối tượng gần nhau nhất trong 2 clusters đó (minimum distance). Xem hình dưới

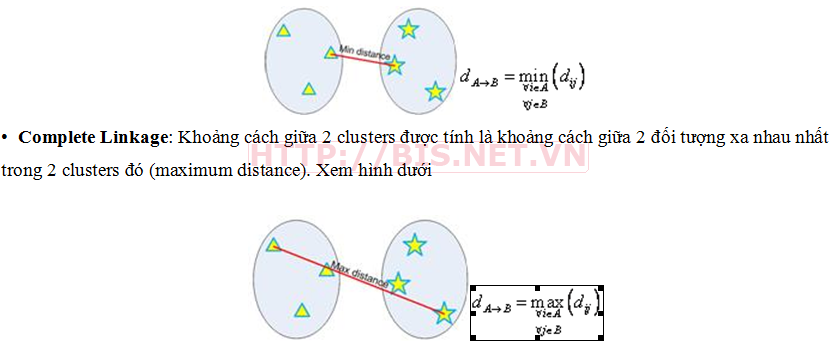
Average Group: Khoảng cách giữa 2 clusters được tính là khoảng cách trung bình giữa các đối tượng trong 2 clusters đó (average distance).Xem hình dưới

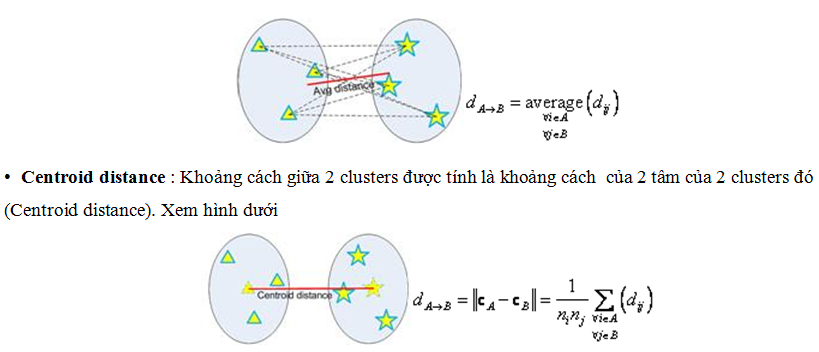
Trong ví dụ này, tôi sử dụng Single Linkage  để xác đinhk khoảng cách giữa 2 clusters.

Trong ví dụ đã cho,  ta có 6 đối tượng (A,B,C,D,E,F). Ban đầu ta xem mỗi đối tượng là 1 cluster. Vì vậy, ban đầu ta có 6 clusters. Mục đích của ta là gộp 6 clusters này lại để đến cuối cùng ta có được 1 cluster bao gồm 6 đối tượng đã cho.

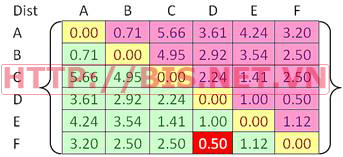
Trong mỗi bước lặp, chúng ta tìm 2 clusters gần nhau nhất (sử dụng Single Linkage) để gộp thành 1 cluster. Trong ví dụ này, ta có cluster D và F là gần nhau nhất (khoảng cách là 0.50) vì vậy ta nhóm D và F vào 1 cluster (D,F). Sau đó tính lại ma trận khoảng cách Dist. Chú ý là khoảng cách giữa các cluster không được nhóm (A,B,C,E) không thay đổi. vấn đề là làm sao để tỉnh khoảng cách từ cluster mới (D,F) đến các clusters khác?.

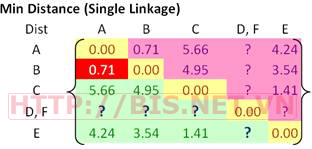
Cập nhật ma trận khoảng cách Dist

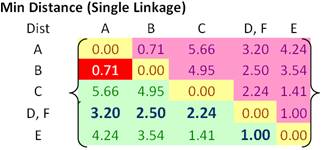
Từ ma trận khoảng cách Dist, ta thấy rằng 2 clusters gần nhau nhất là A và B. Vì vậy ta nhóm A và B thành 1 cluster (A,B)

Tính lại khoảng cách giữa các clusters

Cập nhật ma trận khoảng cách

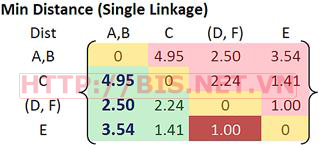
Ta nhóm 2 clusters E và (D,F) thành 1 cluster ((D, F), E ) vì khoảng cách giữa 2 clusters này là nhỏ nhất (1.0)

Cập nhật ma trận khoảng cách như sau

 Cập nhật ma trận khoảng cách như sau

Có thể tổng kết quả các bước tính toán của thuật toán AHC trong ví dụ trên như sau:

1.      Bắt đầu, ta có 6 clusters : A, B, C, D, E và F

2.      Gộp 2 clusters  D và  F thành cluster (D, F) với khoảng cách nhỏ nhất là 0.50

3.      Gộp 2 clusters  A và cluster B thành (A, B) với khoảng cách nhỏ nhất là 0.71

4.      Gộp 2 clusters  E và  (D, F) thành ((D, F), E) với khoảng cách nhỏ nhất là 1.00

5.      Gộp 2 clusters ((D, F), E) và  C thành (((D, F), E), C) với khoảng cách nhỏ nhất là 1.41

6.      Gộp 2 clusters (((D, F), E), C) và (A, B) thành ((((D, F), E), C), (A, B)) với khoảng cách nhỏ nhất là 2.50

7.      Cluster cuối cùng bao gồm tất cả 6 đối tượng ban đầu, thuật toán dừng

Quá trình phân cụm theo thuật toán AHC trong ví dụ trên được minh họa như hình sau:

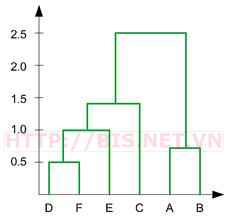
Thứ tự phân cụm như sau (((D, F), E),C), (A,B).

 Kỹ thuật phân nhóm Hierarchical Clustering hiện nay được triển khai trong rất nhiều phần mềm khai phá dữ liệu (Data Mining Softwares) như Weka, XLSTAT, XLMiner, Clementine (của SPSS),….

 PS. All comments please send to chucnv@ud.edu.vn. Thank you and Welcome!