Vấn đề ra quyết định với nhiều điều kiện (Multi Criteria Decision Making)
Nguyễn Văn Chức – chuc.nv@due.edu.vn
Chúng ta đưa ra rất nhiều quyết định trong cuộc đời. Quyết định chọn trường nào để học Đại học, nơi nào để sống, mua loại xe gì, làm nghề gì trong tương lai,…
Ra quyết định là quá trình chọn lựa dựa trên các điều kiện (Criteria hay Factor) trong một tình huống cụ thể. Như vậy, vấn đề quan trọng khi ra quyết định là phải xác định được các điều kiện tác động đến quyết định và cân nhắc, lựa chọn làm sao để có được một quyết định phù hợp nhất.
Bài viết này giới thiệu một số vấn đề cần quan tâm khi lựa chọn quyết định với nhiều điều kiện. Trong bài viết này khái niệm Criteria và Factor có cùng nghĩa là điều kiện ảnh hưởng đến lựa chọn (Alternatives). Bảng dưới đây mô tả các điều kiện cũng như các lựa chọn để ra một quyết định
Khi bạn cố gắng để có được một quyết định tốt nhất trong trường hợp có nhiều điều kiện và nhiều lựa chọn, việc áp dụng các kỹ thuật dưới đây giúp bạn có thể đưa ra quyết định “có lý trí” hơn là dựa vào ý kiến chủ quan của mình.
Cross Tabulation (bảng chéo)
Cách đơn giản nhất để phân tích đối với các quyết định nhiều điều kiện và nhiều lựa chọn là biểu diễn các điều kiện và lựa chọn trong một Cross table. Giả sử ta có 3 lựa chọn (Alternatives) là X, Y và Z và 4 điều kiện (nhân tố) là Factor A, B, C và D được biểu diễn bởi Cross table như sau (Table 2)
Chú ý rằng giá trị của các Factor có thang đo (Range) khác nhau, và trong một Range thì giá trị càng cao thì độ thích hợp (tốt) càng lớn.
Nếu bạn có nhiều lựa chọn, và mỗi lựa chọn được xác định bởi các giá trị trong một Range nhất định thì việc đánh giá các lựa chọn được dựa trên
Normalized Score được tính như sau:
Total sums =150.55 (=19.4+74.75+56.4).
Normalized Score đối với mỗi lựa chọn được tính bằng cách lấy Sum của mỗi lựa chọn chia cho Total sums. Chẳn hạn Normalized Score của Choice X =19.4/150.55*100% =12.9%.
Lựa chọn có giá trị Normalized Score càng lớn thì càng thích hợp (tốt) hơn. Rõ ràng ta thấy rằng lựa chọn Y thích hợp hơn (tốt hơn) lựa chọn Z và lựa chọn Z tốt hơn lựa chọn X. (Nói cách khác lựa chọn Y là thích hợp nhất trong 3 lựa chọn)
Tuy nhiên một điều cần chú ý rằng trong Table 2, thang đo (Range) của mỗi Factor không giống nhau, do đó việc tính tổng giá trị của các factor đối với các giá trị trong các Range khách nhau là không hợp lý. Việc này có thể bị ảnh hưởng bởi các Factor có Range lớn (ví dụ như Range của Factor B trong bảng trên). Để khắc phục nhược điểm này có 2 giải pháp đó là:
- Thay vì sử dụng giá trị bất kỳ của mỗi Factor, chúng ra xếp hạng (Rank) lựa chọn cho mỗi factor. Các lựa chọn có giá trị Rank càng nhỏ thì càng hợp lý (tốt)
- Chúng ta chuyển đổi giá trị Score của mỗi Factor sao cho mỗi Factor có cùng thang đo để so sánh
Đánh giá dựa vào xếp hạng (Rank)((((((
Chúng ta chuyển các giá trị trong Table 2 sang thứ hạng (Rank) như sau:
Vì có 3 lựa chọn nên giá trị của mỗi dòng chỉ nhận những giá trị theo thứ hạng 1 hoặc 2 hoặc 3 (tùy thuộc vào giá trị của chúng trong Table 2)
Sau khi xếp hạng, lựa chọn nào có Rank nhỏ hơn sẽ tốt hơn. Vì vậy Normalized Score được tính theo công thức sau:
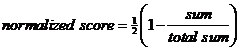
The total sum = 23 (=11+6+6).
Trong ví dụ này Normalized score của Choice X = 0.5*(1-11/23) = 26.09%, Normalized score của Choice Y và Z là 0.5*(1-6/23) = 36.96%.
Giá trị của Normalized Score càng nhỏ thì lựa chọn càng thích hợp hơn. Ta thấy rằng lựa chọn X thích hợp hơn (tốt hơn) lựa chọn Y và Z
Chuyển giá trị của các Factors về cùng thang đo
Thông thường, thang đo chuẩn hóa này chuyển tất cả các giá trị của các Factor về khoảng [0,1]. Công thức chuyển đổi như sau:
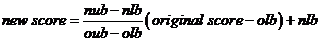
nub: new upper bound (cận trên của thang đo mới)
nlb: new lower bound (cận dưới của thanh đo mới)
olb: original lower bound (Cận dưới của thang đo ban đầu)
oub: original upper bound (cận trên của thang đo ban đầu)
Đồ thị minh họa việc chuyển đổi
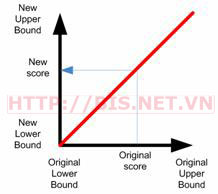
Sử dụng công thức trên, chuyển dữ liệu trong Table 2 như bảng sau:
Ví dụ đối với Factor A ta có: Original range từ 0 đến 5. Để chuyển Score của Choice Y từ 4 vào Range [0,1] ta có: olb = 0, oub = 5, nlb = 0, nub = 1, score = 4, vậy
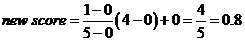 .
.
Ví dụ khác đối với choice X trong Factor B có original score = 20, original range từ 1 đến 100. Vì vậy ta có olb = 1, oub = 100, nlb = 0, nub = 1 and score = 20, vậy
Với việc chuyển đổi này, theo dữ liệu từ Table 4 ta thấy rằng lựa chọn Y là tốt nhất (giá trị cao nhất).
Việc chuyển đổi để cho tất cả các Factor sử dụng chung thang đo (Range) tuy có hơi phức tạp nhưng cho kết quả tốt hơn kỹ thuật dựa vào thứ hạng (Rank)
Các điều kiện có trọng số (Weighted Criteria)
Trong các phân tích trên, ta giả sử rằng các điều kiện (factor) có tác động đến lựa chọn như nhau (có mức độ quan trọng bằng nhau). Tuy nhiên, trong thức tế thì đôi lúc các điều kiện này lại có mức độ quan trọng khác nhau và được biểu diễn bởi trọng số gọi là Importance Weight.
Dữ liệu trong Table 5 có nghĩa là Factor B và C có mức độ quan trọng gấp đôi Factor D và Factor A có mức độ quan trọng gấp 3 Factor B
Trọng số thể hiện mức độ quan trọng của các Factor được chuẩn hóa như bảng sau:
Sau khi có được trọng số (Weight) của mỗi Factor, ta nhân trọng số đó với giá trị chuyển đổi của các Factor trong Table 4 ta có được dữ liệu như Table 6 dưới đây:
Chẳn hạn, với Factor A đối với Choice X, ta có Weight = 54.5%, giá trị chuyển đổi trong thang đo [0,1] là 0.2 (xem Table 4) nên ta có giá trị của Factor A đối với Choice A có tính đến trọng số là 54.5*0.2/100=0.109
So sánh Normalized Score của Table 4 và Table 6 ta có thể nhận thấy có sự thay đổi trong việc lựa chọn. Trong Table 4, lựa chọn Y tốt hơn Z. Tuy nhiên sau khi áp dụng trọng số cho các Factor dữ liệu trong Table 6 giúp ta kết luận rằng lựa chọn Z là tốt nhất trong 3 lựa chọn.
Việc ra quyết định bị ảnh hưởng rất lớn bởi ý kiến chủ quan của người ra quyết định. Vấn đề này đôi lúc gây khó khăn cho việc ra quyết định nhất là trong trường hợp quyết định có nhiều điều kiện và nhiều lựa chọn. Bài viết này giới thiệu các kỹ thuật đơn giản giúp phân tích và đưa ra quyết có tính định lượng và “lý trí” hơn với các ý kiến chủ quan của người ra quyết định.
All comments please send to chucnv@ud.edu.vn. Thank you and Welcome!